We know that quantum computing is coming and that it will have significant impacts for encryption protocols (/content/f5-labs/en/labs/articles/threat-intelligence/how-quantum-computing-will-change-browser-encryption.html). Let’s discuss how much stronger our existing encryption standards need to become to be considered secure in a post-quantum computing (post-QC) world.
Much of the communication that occurs over the Internet today (/content/f5-labs/en/labs/articles/threat-intelligence/the-2016-tls-telemetry-report-24674.html)—anything that relies on SSL/TLS—is dependent on asymmetric encryption algorithms, such as Elliptic Curve Cryptography (ECC), RSA, or finite field operations such as Diffie-Hellman (DH), to ensure security. To determine just how strong that security is in a pre-QC world, we measure against the strength of the block cipher. Table 2 from the NIST Recommendation for Key Management1 is the definitive guide here (some variations of this table are possible, but in general they look like this one):
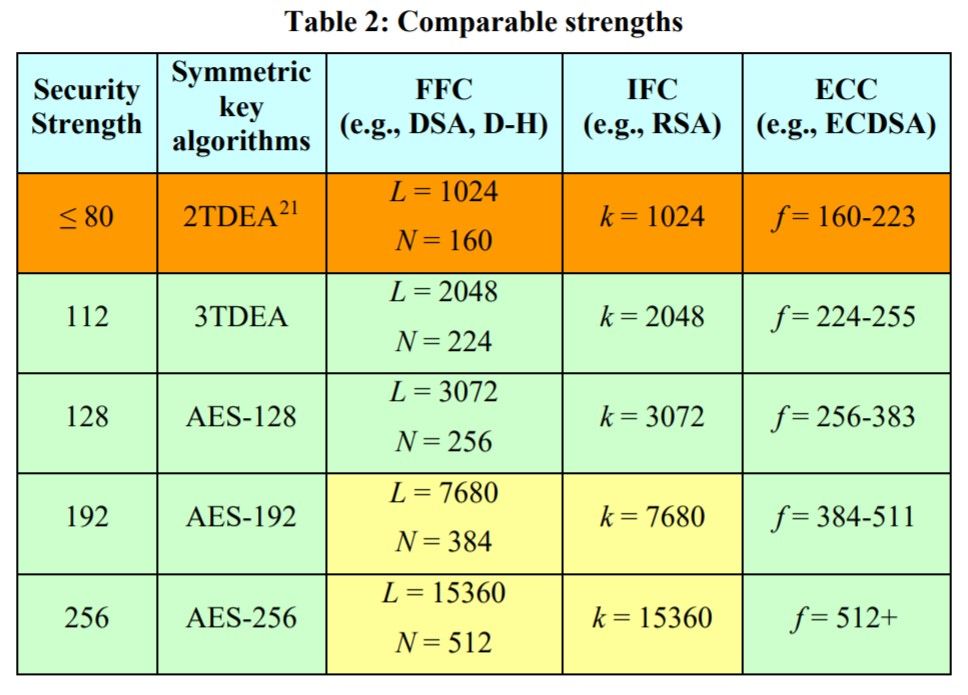
Observe that "standard security," which is AES-128, corresponds to RSA 3072 ("3K"). The next level of security that's most often used is P-384 (current Suite B) / AES-192 or AES-256 / Ed448-Goldilocks,2 and it corresponds to 7.6K – 15K RSA keys. The RSA key length does not scale linearly with security strength. It's incorrect to say that a 4K RSA key is 33% stronger than a 3K RSA key—it's actually much less so. In addition, a rule of thumb is that the performance impact of the longer length is quadratic at least, therefore, for 30% longer RSA keys, we should expect to pay at least a 70% performance penalty. In essence, when increasing key length, security strength increases slower than key length, while performance costs increase faster than key length.
The threat of quantum computers arriving sooner than expected3 somehow clouds this picture. The confusion comes from the idea that ECC will fall a bit sooner than RSA because one can use a QC with fewer qubits, and, therefore, RSA is stronger than ECC, but this is a small advantage in the era of QCs. The need for longer RSA keys comes from existing attacks using old, known algorithms, such as index calculus. RSA is equally broken by a QC at essentially similar effort.
The bottom line is that there is no material difference between 3K and 4K RSA keys for "standard" security level (of AES-128 strength, non-QC security). To get "strong" (non-QC) security, one needs to use large RSA sizes starting from 7K. RSA is not a QC-safe algorithm and should not be viewed as such.
Another point is that with modern protocols like TLS 1.3 or HTTP 2.0 (with TLS 1.2 or TLS 1.3), RSA is only used for authentication, which makes QC issues much less of a concern (because the previously encrypted traffic is not encrypted to the RSA keys in these cases). For this reason, anything above RSA 3K is most likely a waste even with QC, if the DH groups used to encrypt traffic are weak. To put it differently, the strength of DH groups is more of a problem than the RSA signature because this is what QC will attack.
In addition to all of this, 3K RSA keys are very slow for servers to process, and greater key sizes lead to slower communications with disproportionately small gains in security. RSA remains popular specifically because RSA encryption (but not decryption) is much faster than ECC of equivalent strength, and remains most widely supported by certificate authorities and browsers.
The unfavorable scaling of RSA key size and the threat of QC attacks against RSA mean that we will need a replacement in the post-QC era. Fortunately, NIST is currently going through a process to identify suitable algorithms that are secure against QC attack. Unfortunately, post-QC algorithms require even larger key sizes, which will be a challenge that products and protocols will need to overcome.
So, what should we do? Existing RSA encryption is inadequate for the coming post-QC world, but stronger RSA encryption leads to unacceptable performance penalties. Even if we accept the high cost of stronger RSA encryption, weak DH groups are more likely to be attacked with QC, anyway. And NIST is working on the selection of post-QC encryption algorithms, but that process is at best 5 years from completion.
The answer is to take a phased approach. SSL/TLS will be staying with the RSA, ECC, and finite field public key algorithms until large-scale quantum computers start to look more feasible than they do now. Given this reality, security architects should be planning migrations to RSA 3K/4K or ECDSA 256, just as they would have, anyway.
To read more about the NIST post-quantum algorithm selection process, see the paper “How Quantum Computing Will Change Browser Encryption (/content/f5-labs/en/labs/articles/threat-intelligence/how-quantum-computing-will-change-browser-encryption.html)."